Теории управления

Тогда процесс

(1)

называется процессом скользящего среднего. Этот

процесс сформирован полностью из шума (из белого шума)

путем сдвига и весового суммирования.

(- весовые коэффициенты). Сумма (1) генерирует

процесс . Процесс - коррелированный марковский

процесс.

Генератор скользящего среднего для формулы (1)

a

i

x

: i

:

Модель авторегрессии и скользящего среднего

авторегрессия скользящее среднее

генератор генератор

случайного сигнала авторегресии

Здесь - белый шум;

- марковский(модельный)процесс, n=1,2

Между генераторами процесс коррелирован.

Многомерная марковская модель

(1) , где

; ;

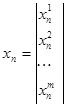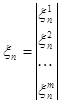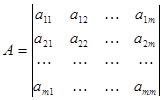
Это самая распространенная модель

(2)

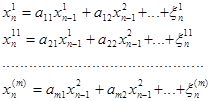
В модели (1) шумы характеризуются матрицей ковариации в

отличие от авторегрессии, под которой понимается следую-

щее:

; ;

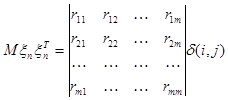- столбец

- строка

Элементы матрицы состоят из корреляции внутри столбика

шума. Столбики между собой коррелированы.

Модель нелинейной регрессии

(3)

(4)

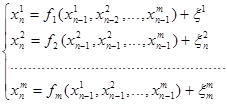
В формулах (3)(матричная форма записи),и (4)(скалярная

 Скачать реферат