Теории управления

З притяжение :

Y F2 ;

К.А. F2 - управляющая сила

F3 - сопротивление среды

;

Третий закон Ньютона :

F3 F1

Если это уравнение спроектировать на оси ко-

ординат, то получим следующие три уравнения :

(1)

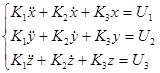
(1)- система линейных дифференциальных уравнений 2-го по-

рядка, которая описывает движение космического аппа-

рата.

Силы U1,U2,U3 - силы управления.

{x(t),y(t),z(t)}r(t) - траектория

Оказывается, что в зависимости от начальных условий и па-

раметров K1,K2,K3 траектория r(t) может быть круговая,

эллипсоидная, параболическая.

Пример 2 : Нелинейная система. Описывается нелинейным дифференциальным уравнением.

Генератор колебаний :

Можно показать, что процесс

x(t) описывается дифферен-

x(t) циальным уравнением 2-го

M порядка с нелинейным

членом .

R

C L L

C Если емкость варьировать,

то может стать ну-

лем и тогда мы получим си-

нусоидальное колебание:

x(t)=a sin(wt+j)

(автоколебания)

Если - положительно, то амплитуда колебаний увели-

чивается с течением времени.

Если - отрицательно - амплитуда колебаний уменьша-

ется с течением времени до нуля.

Математическое описание систем (детерминированная терия) (идеальный случай)

Линейные системы, которые описываются дифференциальными

уравнениями называются динамическими системами.

Если система описывается алгебраическими уравнениями -

- это описание состояния равновесия (статические системы)

По определению

(1)

(1)- линейное дифференциальное уравнение n-го порядка.

Правая часть - это дифференциальное уравнение воз-

действия. Если Ly=0 (2) ,то Ly=Px.

(2)- однородное дифференциальное уравнение - описывает

линейные динамические системы без воздействия на

них. Например колебательный контур.

Правая часть уравнения (1) описывает воздействие на ли-

нейную систему или называется управлением.

Ly=x - управление.

Если есть часть Px - то это сложное управление, учитыва-

 Скачать реферат