Теории управления

1 2 3 4 5 n t

а=1 - модель взрыва. Если - гауссовский случайный про-

цесс, то легко доказать, что многомерная ФПВ факторизует-

ся.

а - коэффициент регрессии.

Если 0<a<1, то можно доказать, что а - это коэффициент

корреляций между и .

Если процесс изменяется очень медленно, то он сильно кор-

релирован. Коррелированными процессами очень легко управ-

лять и они очень легко анализируются и прогнозируются.

Генератор марковского процесса, реализующий авторегрессию

1-го порядка

(1)

Генератор

- марковский случайный процесс

- генератор случайных чисел (в ЭВМ)

i = 0,1,2 .n

Утверждение (1) : процесс (1) является марковским.

Доказательство: Пусть заданная величина. Процедура (1) называется реккурсивной или иттеративной, рекурент-

ной.

(2)

Пусть ~, где 0-среднее, - дисперсия.

В формуле (2) разность имеет гауссовкий процесс распре-

деления или :

(3)

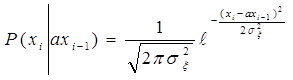
(4)

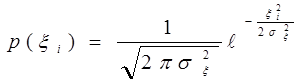
(3) получено из (4) и (2) заменив на . Поскольку

- независимые по условию, то имеем :

Утверждение доказано. Процесс (1) является марковским.

Структурная схема генератора марковского процесса

реализация рекурсии

a |¾¾| рис. 1

T

|¾¾| - линия задержки.

Это структурная схема 4х полюсника, которая реализует

генерацию марковского случайного процесса . Это генера-

тор с внешним возбуждением, который возбуждается с по-

мощью независимого гауссовского процесса .

Сетка дискретного времени:

|¾¾|¾¾|¾¾|¾¾® t

T

Утверждение (2)

На выходе 4х полюсника процесс ,i=1,2 .n - коррелиро-

ван, с коэффициентом корреляции ‘a’.

Доказательство: Из (1) имеем , берем мат-

ожидание, ,

, - коэффициент корреляции.

 Скачать реферат