Управление ресурсами предприятия
6
Цикл №3.
Поскольку в данном случае интенсивный фактор относится к логарифмическому типу, оптимальное значение параметра управления в первом цикле будет находиться в интервале![]() у.е.ст. Для вычисления точного значения воспользуемся методом “фиктивных” точек. Сформируем последовательность F0=F1=1, F2=2, F3=3, F4=3+2=5, F5=5+3=8, F6=8+5=13, F7=13+8=21, F8=21+13=34, F9=34+21=55, F10=55+34=89, F11=144. Отсюда определяем n = 11. Для удобства дальнейших вычислений сформированную последовательность запишем следующим образом Fn=144, Fn-1=89, Fn-2=55, Fn-3=34, Fn-4=21, Fn-5=13, Fn-6=8, Fn-7=5, Fn-8=3, Fn-9=2, Fn-10=1.
у.е.ст. Для вычисления точного значения воспользуемся методом “фиктивных” точек. Сформируем последовательность F0=F1=1, F2=2, F3=3, F4=3+2=5, F5=5+3=8, F6=8+5=13, F7=13+8=21, F8=21+13=34, F9=34+21=55, F10=55+34=89, F11=144. Отсюда определяем n = 11. Для удобства дальнейших вычислений сформированную последовательность запишем следующим образом Fn=144, Fn-1=89, Fn-2=55, Fn-3=34, Fn-4=21, Fn-5=13, Fn-6=8, Fn-7=5, Fn-8=3, Fn-9=2, Fn-10=1.
Вычислим значение целевой функции в точках
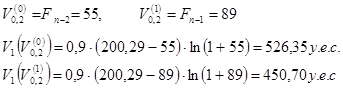
Поскольку целевая функция имеет большее значение в точке ![]() , то это значение функции запоминается, а следующее приближение значения
, то это значение функции запоминается, а следующее приближение значения![]() определяется по формуле
определяется по формуле
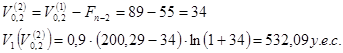
Сравнивая ![]() и
и ![]() запоминаем большее значение, а следующее значение целевой функции вычисляем в точке
запоминаем большее значение, а следующее значение целевой функции вычисляем в точке
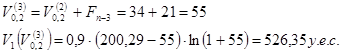
Сравнивая значения целевой функции в точках ![]() и
и ![]() устанавливаем, что значение в точке
устанавливаем, что значение в точке ![]() оказывается лидирующим. Поэтому в следующем шаге приближение к
оказывается лидирующим. Поэтому в следующем шаге приближение к ![]() вычисляется по формуле
вычисляется по формуле
![]()
![]()
Сравнение значений целевой функции в точках ![]() и
и ![]() оказывается в пользу приближения
оказывается в пользу приближения ![]() . Поэтому в очередном шаге абсцисса следующего значения определяется по формуле
. Поэтому в очередном шаге абсцисса следующего значения определяется по формуле
![]()
Вычисляя значение целевой функции в точке ![]() , получим
, получим
![]()
Поскольку значение целевой функции оказалось меньшим, чем в точке ![]() , то абсцисса следующего значения определяется по формуле
, то абсцисса следующего значения определяется по формуле
![]()
Соответствующее значение целевой функции равно
![]()
![]()
Поскольку значение целевой функции снова оказалось меньшим, чем в точке ![]() , то абсцисса следующего значения определяется по формуле
, то абсцисса следующего значения определяется по формуле
![]()
Соответствующее значение целевой функции равно
![]()
Процесс вычисления точного значения можно считать завершенным, т.к. последнее значение абсциссы совпало с уже вычисленным на пятом этапе
Прирост прибыли и коэффициент прироста прибыли составляют соответственно ![]() у.е.с. и
у.е.с. и ![]()
Аналитическая часть.
Для проведения сравнительного анализ построим сводную таблицу в которую внесём данные о приростах прибыли по каждому сегменту, циклу.
| Циклы | Сегменты рынка | |||||
| № 1 | № 2 | |||||
| Прибыль | Прирост | к | Прибыль | Прирост | к | |
| у.е.с. | у.е.с. | у.е.с. | у.е.с. | |||
| Начальный капитал | 52 | - | - | 52 | - | - |
| 1 | 41,16 | -10,84 | 0,79 | 92,63 | 40,63 | 1,78 |
| 2 | 29,88 | -11,28 | 0,73 | 200,29 | 107,66 | 2,16 |
| 3 | 29,23 | -0,65 | 0,98 | 535,82 | 335,53 | 2,68 |
На основании сводной таблицы можно сделать следующие выводы:
- Очевидно, что первый сегмент рынка убыточен (в сумме убытки составляют 52-29,23=22,77 у.е.с.). Это можно объяснить небольшим коэффициентом эффективности экстенсивных инвестиций (0,4). При расчёте установлено оптимально распределение совокупных ресурсов, при котором величина убытков минимальна.
- Втором сегмент рынка интересен с точки зрения получения прибыльности (прирост прибыли составляет 480,82 у.е.с.)
- Самым эффективным циклом и в первом и во втором сегменте является 3-й цикл. Действительно, с первом сегменте имеем самый минимальный убыток (0,65 у.е.с.), а во втором сегменте самый большой прирост прибыли (335,53 у.е.с.)
