Управление ресурсами предприятия
4
![]()
Вычисляя значение целевой функции в точке ![]() , получим
, получим
![]()
Поскольку значение целевой функции оказалось меньшим, чем в точке ![]() , то абсцисса следующего значения определяется по формуле
, то абсцисса следующего значения определяется по формуле
![]()
Соответствующее значение целевой функции равно
![]()
Поскольку значение целевой функции оказалось меньшим, чем в точке ![]() , то абсцисса следующего значения определяется по формуле
, то абсцисса следующего значения определяется по формуле
![]()
Соответствующее значение целевой функции равно
![]()
Процесс вычисления точного значения можно считать завершенным, т.к. последнее значение абсциссы совпало с уже вычисленным на первом этапе
Цикл №2.
Поскольку в данном случае интенсивный фактор относится к логарифмическому типу, оптимальное значение параметра управления в первом цикле будет находиться в интервале![]() у.е.ст. Для вычисления точного значения воспользуемся методом “фиктивных” точек. Сформируем последовательность F0=F1=1, F2=2, F3=3, F4=3+2=5, F5=5+3=8, F6=8+5=13, F7=13+8=21. Отсюда определяем n = 7. Для удобства дальнейших вычислений сформированную последовательность запишем следующим образом Fn=21, Fn-1=13, Fn-2=8, Fn-3=5, Fn-4=3, Fn-5=2, Fn-6=1.
у.е.ст. Для вычисления точного значения воспользуемся методом “фиктивных” точек. Сформируем последовательность F0=F1=1, F2=2, F3=3, F4=3+2=5, F5=5+3=8, F6=8+5=13, F7=13+8=21. Отсюда определяем n = 7. Для удобства дальнейших вычислений сформированную последовательность запишем следующим образом Fn=21, Fn-1=13, Fn-2=8, Fn-3=5, Fn-4=3, Fn-5=2, Fn-6=1.
Вычислим значение целевой функции в точках
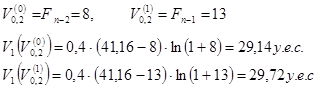
Поскольку целевая функция имеет большее значение в точке ![]() , то это значение функции запоминается, а следующее приближение значения
, то это значение функции запоминается, а следующее приближение значения![]() определяется по формуле
определяется по формуле
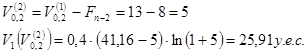
Сравнивая ![]() и
и ![]() запоминаем большее значение, а следующее значение целевой функции вычисляем в точке
запоминаем большее значение, а следующее значение целевой функции вычисляем в точке
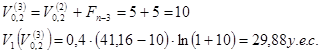
Сравнивая значения целевой функции в точках ![]() и
и ![]() устанавливаем, что значение в точке
устанавливаем, что значение в точке ![]() оказывается лидирующим. Поэтому в следующем шаге приближение к
оказывается лидирующим. Поэтому в следующем шаге приближение к ![]() вычисляется по формуле
вычисляется по формуле
![]()
![]()
Сравнение значений целевой функции в точках ![]() и
и ![]() оказывается в пользу приближения
оказывается в пользу приближения ![]() . Поэтому в очередном шаге абсцисса следующего значения определяется по формуле
. Поэтому в очередном шаге абсцисса следующего значения определяется по формуле
![]()
Вычисляя значение целевой функции в точке ![]() , получим
, получим
![]()
Поскольку значение целевой функции оказалось меньшим, чем в точке ![]() , то абсцисса следующего значения определяется по формуле
, то абсцисса следующего значения определяется по формуле
![]()
Соответствующее значение целевой функции равно
![]()
Процесс вычисления точного значения можно считать завершенным, т.к. последнее значение абсциссы совпало с уже вычисленным на третьем этапе
Цикл №3.
Поскольку в данном случае интенсивный фактор относится к логарифмическому типу, оптимальное значение параметра управления в первом цикле будет находиться в интервале![]() у.е.ст. Для вычисления точного значения воспользуемся методом “фиктивных” точек. Сформируем последовательность F0=F1=1, F2=2, F3=3, F4=3+2=5, F5=5+3=8, F6=8+5=13, F7=13+8=21. Отсюда определяем n = 7. Для удобства дальнейших вычислений сформированную последовательность запишем следующим образом Fn=21, Fn-1=13, Fn-2=8, Fn-3=5, Fn-4=3, Fn-5=2, Fn-6=1.
у.е.ст. Для вычисления точного значения воспользуемся методом “фиктивных” точек. Сформируем последовательность F0=F1=1, F2=2, F3=3, F4=3+2=5, F5=5+3=8, F6=8+5=13, F7=13+8=21. Отсюда определяем n = 7. Для удобства дальнейших вычислений сформированную последовательность запишем следующим образом Fn=21, Fn-1=13, Fn-2=8, Fn-3=5, Fn-4=3, Fn-5=2, Fn-6=1.
Вычислим значение целевой функции в точках
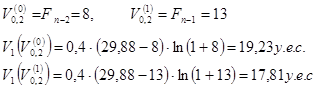
Поскольку целевая функция имеет большее значение в точке ![]() , то это значение функции запоминается, а следующее приближение значения
, то это значение функции запоминается, а следующее приближение значения![]() определяется по формуле
определяется по формуле
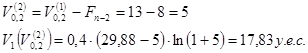
Сравнивая ![]() и
и ![]() запоминаем большее значение, а следующее значение целевой функции вычисляем в точке
запоминаем большее значение, а следующее значение целевой функции вычисляем в точке
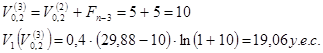
Сравнивая значения целевой функции в точках ![]() и
и ![]() устанавливаем, что значение в точке
устанавливаем, что значение в точке ![]() оказывается лидирующим. Поэтому в следующем шаге приближение к
оказывается лидирующим. Поэтому в следующем шаге приближение к ![]() вычисляется по формуле
вычисляется по формуле
![]()
![]()
Сравнение значений целевой функции в точках ![]() и
и ![]() оказывается в пользу приближения
оказывается в пользу приближения ![]() . Поэтому в очередном шаге абсцисса следующего значения определяется по формуле
. Поэтому в очередном шаге абсцисса следующего значения определяется по формуле
![]()
Вычисляя значение целевой функции в точке ![]() , получим
, получим
![]()
