Анализ затрат на качество продукции
7
Степень взаимосвязи между какими-либо характеристиками качества, имеющими количественное выражение, и затратами на него или ценой изделия в целом как формой его стоимости, в которой основной удельный вес занимают затраты, позволяет определить коэффициент корреляции. Его можно исчислить по формуле:
 где
где

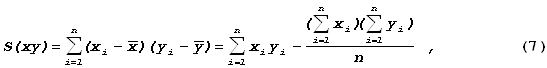
где n – число пар данных; S(xy) называется ковариацией; x и y – два исследуемых показателями.
Коэффициент корреляции может принимать значения от –1 до +1. При r, близком к │1│, можно говорить о высокой степени тесноты связи между исследуемыми переменными и напротив: при r, близком к 0, корреляция между ними выражена слабо. Если r = │1│, все точки на диаграмме рассеивания будут лежать на одной прямой. Если же r = 0, корреляционная связь между факторным и результативным показателями отсутствует. Знак «+» или «–» говорит о направлении связи – прямом или обратном. По формулам (4) – (7) и данным табл. 1 можно найти коэффициент корреляции. Дополнительные необходимые расчеты приведены в табл. 5. Тогда, подставив полученные значения, будем иметь:
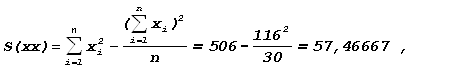
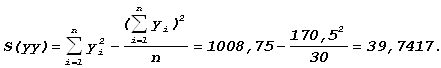
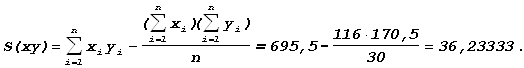
Отсюда
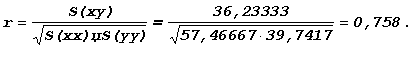 |
Значение r, равное +0,758, свидетельствует о наличии высокой положительной корреляции между упаковкой товара, являющейся одним из показателей его качества, и ценой на него, в которой воплощены затраты на товар, что подтверждает предварительный вывод, сделанный по диаграмме рассеивания.
Таблица 5
Показатели для расчета коэффициента корреляции
| X | X2 |
Y | Y2 | XY |
| 1 | 1 | 4 | 16 | 4 |
| 2 | 4 | 4 | 16 | 8 |
| 2 | 4 | 4,5 | 20,25 | 9 |
| 3 | 9 | 4,5 | 20,25 | 13,5 |
| 4 | 16 | 6 | 36 | 24 |
| 5 | 25 | 8 | 64 | 40 |
| 3 | 9 | 5,5 | 30,25 | 16,5 |
| 4 | 16 | 5,5 | 30,25 | 22 |
| 5 | 25 | 5,5 | 30,25 | 27,5 |
| 2 | 4 | 5 | 25 | 10 |
| 3 | 9 | 5 | 25 | 15 |
| 3 | 9 | 5 | 25 | 15 |
| 5 | 25 | 7 | 49 | 35 |
| 6 | 36 | 7 | 49 | 42 |
| 6 | 36 | 7,5 | 56,25 | 45 |
| 3 | 9 | 4 | 16 | 12 |
| 1 | 1 | 4,5 | 20,25 | 4,5 |
| 5 | 25 | 6 | 36 | 30 |
| 5 | 25 | 6 | 36 | 30 |
| 5 | 25 | 7,5 | 56,25 | 37,5 |
| 3 | 9 | 5,5 | 30,25 | 16,5 |
| 4 | 16 | 5,5 | 30,25 | 22 |
| 5 | 25 | 5,5 | 30,25 | 27,5 |
| 4 | 16 | 4,5 | 20,25 | 18 |
| 3 | 9 | 6,5 | 42,25 | 19,5 |
| 4 | 16 | 6,5 | 42,25 | 26 |
| 5 | 25 | 6,5 | 42,25 | 32,5 |
| 6 | 36 | 8 | 64 | 48 |
| 4 | 16 | 5 | 25 | 20 |
| 5 | 25 | 5 | 25 | 25 |
| ∑116 | ∑506 | ∑170,5 | ∑1008,75 | ∑695,5 |
